Boost  v1.57.0
doxygen for www.boost.org
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Modules Pages
Public Types | Public Member Functions | List of all members
boost::accumulators::impl::skewness_impl< Sample > Struct Template Reference

Skewness estimation. More...

#include <statistics_fwd.hpp>

Inheritance diagram for boost::accumulators::impl::skewness_impl< Sample >:
Inheritance graph
[legend]
Collaboration diagram for boost::accumulators::impl::skewness_impl< Sample >:
Collaboration graph
[legend]

Public Types

typedef
numeric::functional::fdiv
< Sample, Sample >
::result_type 		result_type
 
typedef mpl::false_ is_droppable
 

Public Member Functions

 skewness_impl (dont_care)
 
template<typename Args >
result_type result (Args const &args) const
 
detail::void_ operator() (dont_care)
 
detail::void_ add_ref (dont_care)
 
detail::void_ drop (dont_care)
 
detail::void_ on_drop (dont_care)
 

Detailed Description

template<typename Sample>
struct boost::accumulators::impl::skewness_impl< Sample >

Skewness estimation.

The skewness of a sample distribution is defined as the ratio of the 3rd central moment and the 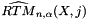$ 3/2 $-th power of the 2nd central moment (the variance) of the samples 3. The skewness can also be expressed by the simple moments:

\[ \hat{g}_1 = \frac {\widehat{m}_n^{(3)}-3\widehat{m}_n^{(2)}\hat{\mu}_n+2\hat{\mu}_n^3} {\left(\widehat{m}_n^{(2)} - \hat{\mu}_n^{2}\right)^{3/2}} \]

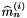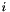where $ \widehat{m}_n^{(i)} $ are the $ i $-th moment and 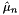$ \hat{\mu}_n $ the mean (first moment) of the 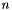$ n $ samples.

Member Typedef Documentation

typedef mpl::false_ boost::accumulators::accumulator_base::is_droppable
inherited
template<typename Sample >
typedef numeric::functional::fdiv<Sample, Sample>::result_type boost::accumulators::impl::skewness_impl< Sample >::result_type

Constructor & Destructor Documentation

template<typename Sample >
boost::accumulators::impl::skewness_impl< Sample >::skewness_impl ( dont_care  )
inline

Member Function Documentation

detail::void_ boost::accumulators::accumulator_base::add_ref ( dont_care  )
inlineinherited
detail::void_ boost::accumulators::accumulator_base::drop ( dont_care  )
inlineinherited
detail::void_ boost::accumulators::accumulator_base::on_drop ( dont_care  )
inlineinherited
detail::void_ boost::accumulators::accumulator_base::operator() ( dont_care  )
inlineinherited
template<typename Sample >
template<typename Args >
result_type boost::accumulators::impl::skewness_impl< Sample >::result ( Args const &  args) const
inline

References boost::accumulators::extract::mean, and boost::geometry::math::sqrt().

The documentation for this struct was generated from the following file: