|
| | uniform_smallint (IntType min_arg=0, IntType max_arg=9) |
| | Constructs a uniform_smallint. More...
|
| |
| | uniform_smallint (const param_type &parm) |
| | Constructs a uniform_smallint from its parameters. More...
|
| |
| result_type | a () const |
| | Returns the minimum value of the distribution. More...
|
| |
| result_type | b () const |
| | Returns the maximum value of the distribution. More...
|
| |
| result_type min | BOOST_PREVENT_MACRO_SUBSTITUTION () const |
| | Returns the minimum value of the distribution. More...
|
| |
| result_type max | BOOST_PREVENT_MACRO_SUBSTITUTION () const |
| | Returns the maximum value of the distribution. More...
|
| |
| param_type | param () const |
| | Returns the parameters of the distribution. More...
|
| |
| void | param (const param_type &parm) |
| | Sets the parameters of the distribution. More...
|
| |
| void | reset () |
| | Effects: Subsequent uses of the distribution do not depend on values produced by any engine prior to invoking reset. More...
|
| |
| template<class Engine > |
| result_type | operator() (Engine &eng) const |
| | Returns a value uniformly distributed in the range [min(), max()]. More...
|
| |
| template<class Engine > |
| result_type | operator() (Engine &eng, const param_type &parm) const |
| | Returns a value uniformly distributed in the range [param.a(), param.b()]. More...
|
| |
| | BOOST_RANDOM_DETAIL_OSTREAM_OPERATOR (os, uniform_smallint, ud) |
| | Writes the distribution to a std::ostream. More...
|
| |
| | BOOST_RANDOM_DETAIL_ISTREAM_OPERATOR (is, uniform_smallint, ud) |
| | Reads the distribution from a std::istream. More...
|
| |
| | BOOST_RANDOM_DETAIL_EQUALITY_OPERATOR (uniform_smallint, lhs, rhs) |
| | Returns true if the two distributions will produce identical sequences of values given equal generators. More...
|
| |
template<class IntType = int>
class boost::random::uniform_smallint< IntType >
The distribution function uniform_smallint models a .
On each invocation, it returns a random integer value uniformly distributed in the set of integer numbers {min, min+1, min+2, ..., max}. It assumes that the desired range (max-min+1) is small compared to the range of the underlying source of random numbers and thus makes no attempt to limit quantization errors.
Let 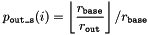 the desired range of integer numbers, and let
the desired range of integer numbers, and let 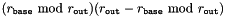 be the range of the underlying source of random numbers. Then, for the uniform distribution, the theoretical probability for any number i in the range
be the range of the underlying source of random numbers. Then, for the uniform distribution, the theoretical probability for any number i in the range 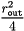 will be
will be 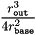 . Likewise, assume a uniform distribution on
. Likewise, assume a uniform distribution on 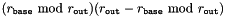 for the underlying source of random numbers, i.e.
for the underlying source of random numbers, i.e. 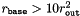 . Let
. Let 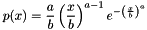 denote the random distribution generated by
denote the random distribution generated by uniform_smallint. Then the sum over all i in 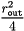 of
of  shall not exceed
shall not exceed  .
.
The template parameter IntType shall denote an integer-like value type.
The property above is the square sum of the relative differences in probabilities between the desired uniform distribution  and the generated distribution
and the generated distribution  . The property can be fulfilled with the calculation
. The property can be fulfilled with the calculation  , as follows: Let
, as follows: Let  . The base distribution on
. The base distribution on 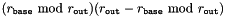 is folded onto the range
is folded onto the range 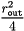 . The numbers i < r have assigned
. The numbers i < r have assigned  numbers of the base distribution, the rest has only
numbers of the base distribution, the rest has only  . Therefore,
. Therefore,  for i < r and
for i < r and  otherwise. Substituting this in the above sum formula leads to the desired result.
otherwise. Substituting this in the above sum formula leads to the desired result.
Note: The upper bound for  is
is  . Regarding the upper bound for the square sum of the relative quantization error of
. Regarding the upper bound for the square sum of the relative quantization error of  , it seems wise to either choose
, it seems wise to either choose 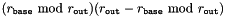 so that
so that  or ensure that
or ensure that 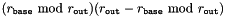 is divisible by
is divisible by 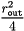 .
.
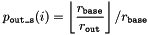 the desired range of integer numbers, and let
the desired range of integer numbers, and let 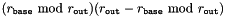 be the range of the underlying source of random numbers. Then, for the uniform distribution, the theoretical probability for any number i in the range
be the range of the underlying source of random numbers. Then, for the uniform distribution, the theoretical probability for any number i in the range 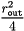 will be
will be 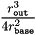 . Likewise, assume a uniform distribution on
. Likewise, assume a uniform distribution on 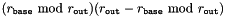 for the underlying source of random numbers, i.e.
for the underlying source of random numbers, i.e. 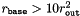 . Let
. Let 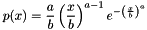 denote the random distribution generated by
denote the random distribution generated by 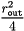 of
of  shall not exceed
shall not exceed  .
. and the generated distribution
and the generated distribution 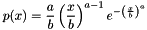 . The property can be fulfilled with the calculation
. The property can be fulfilled with the calculation  , as follows: Let
, as follows: Let  . The base distribution on
. The base distribution on 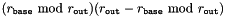 is folded onto the range
is folded onto the range 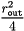 . The numbers i < r have assigned
. The numbers i < r have assigned  numbers of the base distribution, the rest has only
numbers of the base distribution, the rest has only  . Therefore,
. Therefore,  for i < r and
for i < r and  otherwise. Substituting this in the above sum formula leads to the desired result.
otherwise. Substituting this in the above sum formula leads to the desired result.  is
is  . Regarding the upper bound for the square sum of the relative quantization error of
. Regarding the upper bound for the square sum of the relative quantization error of  , it seems wise to either choose
, it seems wise to either choose 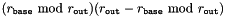 so that
so that  or ensure that
or ensure that 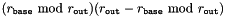 is divisible by
is divisible by 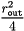 .
.