Boost  v1.57.0
doxygen for www.boost.org
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Modules Pages
Public Types | Public Member Functions | List of all members
boost::accumulators::impl::weighted_skewness_impl< Sample, Weight > Struct Template Reference

Skewness estimation for weighted samples. More...

#include <statistics_fwd.hpp>

Inheritance diagram for boost::accumulators::impl::weighted_skewness_impl< Sample, Weight >:
Inheritance graph
[legend]
Collaboration diagram for boost::accumulators::impl::weighted_skewness_impl< Sample, Weight >:
Collaboration graph
[legend]

Public Types

typedef
numeric::functional::multiplies
< Sample, Weight >
::result_type 		weighted_sample
 
typedef
numeric::functional::fdiv
< weighted_sample,
weighted_sample >::result_type 		result_type
 
typedef mpl::false_ is_droppable
 

Public Member Functions

 weighted_skewness_impl (dont_care)
 
template<typename Args >
result_type result (Args const &args) const
 
detail::void_ operator() (dont_care)
 
detail::void_ add_ref (dont_care)
 
detail::void_ drop (dont_care)
 
detail::void_ on_drop (dont_care)
 

Detailed Description

template<typename Sample, typename Weight>
struct boost::accumulators::impl::weighted_skewness_impl< Sample, Weight >

Skewness estimation for weighted samples.

The skewness of a sample distribution is defined as the ratio of the 3rd central moment and the 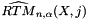$ 3/2 $-th power $ of the 2nd central moment (the variance) of the samples. The skewness can also be expressed by the simple moments:

\[ \hat{g}_1 = \frac {\widehat{m}_n^{(3)}-3\widehat{m}_n^{(2)}\hat{\mu}_n+2\hat{\mu}_n^3} {\left(\widehat{m}_n^{(2)} - \hat{\mu}_n^{2}\right)^{3/2}} \]

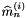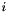where $ \widehat{m}_n^{(i)} $ are the $ i $-th moment and 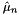$ \hat{\mu}_n $ the mean (first moment) of the 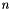$ n $ samples.

The skewness estimator for weighted samples is formally identical to the estimator for unweighted samples, except that the weighted counterparts of all measures it depends on are to be taken.

Member Typedef Documentation

typedef mpl::false_ boost::accumulators::accumulator_base::is_droppable
inherited
template<typename Sample , typename Weight >
typedef numeric::functional::fdiv<weighted_sample, weighted_sample>::result_type boost::accumulators::impl::weighted_skewness_impl< Sample, Weight >::result_type
template<typename Sample , typename Weight >
typedef numeric::functional::multiplies<Sample, Weight>::result_type boost::accumulators::impl::weighted_skewness_impl< Sample, Weight >::weighted_sample

Constructor & Destructor Documentation

template<typename Sample , typename Weight >
boost::accumulators::impl::weighted_skewness_impl< Sample, Weight >::weighted_skewness_impl ( dont_care  )
inline

Member Function Documentation

detail::void_ boost::accumulators::accumulator_base::add_ref ( dont_care  )
inlineinherited
detail::void_ boost::accumulators::accumulator_base::drop ( dont_care  )
inlineinherited
detail::void_ boost::accumulators::accumulator_base::on_drop ( dont_care  )
inlineinherited
detail::void_ boost::accumulators::accumulator_base::operator() ( dont_care  )
inlineinherited
template<typename Sample , typename Weight >
template<typename Args >
result_type boost::accumulators::impl::weighted_skewness_impl< Sample, Weight >::result ( Args const &  args) const
inline

References boost::geometry::math::sqrt(), and boost::accumulators::extract::weighted_mean.

The documentation for this struct was generated from the following file: