Boost  v1.57.0
doxygen for www.boost.org
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Modules Pages
Public Types | Public Member Functions | List of all members
boost::accumulators::impl::peaks_over_threshold_impl< Sample, LeftRight > Struct Template Reference

Peaks over Threshold Method for Quantile and Tail Mean Estimation. More...

#include <peaks_over_threshold.hpp>

Inheritance diagram for boost::accumulators::impl::peaks_over_threshold_impl< Sample, LeftRight >:
Inheritance graph
[legend]
Collaboration diagram for boost::accumulators::impl::peaks_over_threshold_impl< Sample, LeftRight >:
Collaboration graph
[legend]

Public Types

typedef
numeric::functional::fdiv
< Sample, std::size_t >
::result_type 		float_type
 
typedef boost::tuple
< float_type, float_type,
float_type > 		result_type
 
typedef mpl::int_< is_same
< LeftRight, left >::value?-1:1 > 		sign
 
typedef mpl::false_ is_droppable
 

Public Member Functions

template<typename Args >
 peaks_over_threshold_impl (Args const &args)
 
template<typename Args >
void operator() (Args const &args)
 
template<typename Args >
result_type result (Args const &args) const
 
detail::void_ operator() (dont_care)
 
detail::void_ add_ref (dont_care)
 
detail::void_ drop (dont_care)
 
detail::void_ on_drop (dont_care)
 

Detailed Description

template<typename Sample, typename LeftRight>
struct boost::accumulators::impl::peaks_over_threshold_impl< Sample, LeftRight >

Peaks over Threshold Method for Quantile and Tail Mean Estimation.

According to the theorem of Pickands-Balkema-de Haan, the distribution function 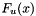$F_u(x)$ of the excesses 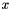$x$ over some sufficiently high threshold 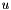$u$ of a distribution function 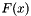$F(x)$ may be approximated by a generalized Pareto distribution

\[ G_{\xi,\beta}(x) = \left\{ \begin{array}{ll} \beta^{-1}\left(1+\frac{\xi x}{\beta}\right)^{-1/\xi-1} & \textrm{if }\xi\neq0\\ \beta^{-1}\exp\left(-\frac{x}{\beta}\right) & \textrm{if }\xi=0, \end{array} \right. \]

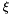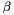with suitable parameters $\xi$ and $\beta$ that can be estimated, e.g., with the method of moments, cf. Hosking and Wallis (1987),

\[ \begin{array}{lll} \hat{\xi} & = & \frac{1}{2}\left[1-\frac{(\hat{\mu}-u)^2}{\hat{\sigma}^2}\right]\\ \hat{\beta} & = & \frac{\hat{\mu}-u}{2}\left[\frac{(\hat{\mu}-u)^2}{\hat{\sigma}^2}+1\right], \end{array} \]

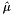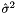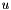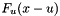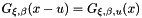$\hat{\mu}$ and $\hat{\sigma}^2$ being the empirical mean and variance of the samples over the threshold $u$. Equivalently, the distribution function $F_u(x-u)$ of the exceedances $x-u$ can be approximated by $G_{\xi,\beta}(x-u)=G_{\xi,\beta,u}(x)$. Since for 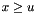$x\geq u$ the distribution function 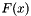$F(x)$ can be written as

\[ F(x) = [1 - \P(X \leq u)]F_u(x - u) + \P(X \leq u) \]

and the probability 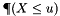$\P(X \leq u)$ can be approximated by the empirical distribution function 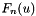$F_n(u)$ evaluated at 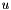$u$, an estimator of 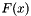$F(x)$ is given by

\[ \widehat{F}(x) = [1 - F_n(u)]G_{\xi,\beta,u}(x) + F_n(u). \]

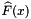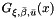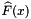It can be shown that $\widehat{F}(x)$ is a generalized Pareto distribution $G_{\xi,\bar{\beta},\bar{u}}(x)$ with $\bar{\beta}=\beta[1-F_n(u)]^{\xi}$ and $\bar{u}=u-\bar{\beta}\left\{[1-F_n(u)]^{-\xi}-1\right\}/\xi$. By inverting $\widehat{F}(x)$, one obtains an estimator for the 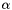$\alpha$-quantile,

\[ \hat{q}_{\alpha} = \bar{u} + \frac{\bar{\beta}}{\xi}\left[(1-\alpha)^{-\xi}-1\right], \]

and similarly an estimator for the (coherent) tail mean,

\[ \widehat{CTM}_{\alpha} = \hat{q}_{\alpha} - \frac{\bar{\beta}}{\xi-1}(1-\alpha)^{-\xi}, \]

cf. McNeil and Frey (2000).

Note that in case extreme values of the left tail are fitted, the distribution is mirrored with respect to the 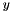$y$ axis such that the left tail can be treated as a right tail. The computed fit parameters thus define the Pareto distribution that fits the mirrored left tail. When quantities like a quantile or a tail mean are computed using the fit parameters obtained from the mirrored data, the result is mirrored back, yielding the correct result.

For further details, see

J. R. M. Hosking and J. R. Wallis, Parameter and quantile estimation for the generalized Pareto distribution, Technometrics, Volume 29, 1987, p. 339-349

A. J. McNeil and R. Frey, Estimation of Tail-Related Risk Measures for Heteroscedastic Financial Time Series: an Extreme Value Approach, Journal of Empirical Finance, Volume 7, 2000, p. 271-300

Parameters
quantile_probability
pot_threshold_value

Member Typedef Documentation

template<typename Sample , typename LeftRight >
typedef numeric::functional::fdiv<Sample, std::size_t>::result_type boost::accumulators::impl::peaks_over_threshold_impl< Sample, LeftRight >::float_type
typedef mpl::false_ boost::accumulators::accumulator_base::is_droppable
inherited
template<typename Sample , typename LeftRight >
typedef boost::tuple<float_type, float_type, float_type> boost::accumulators::impl::peaks_over_threshold_impl< Sample, LeftRight >::result_type
template<typename Sample , typename LeftRight >
typedef mpl::int_<is_same<LeftRight, left>::value ? -1 : 1> boost::accumulators::impl::peaks_over_threshold_impl< Sample, LeftRight >::sign

Constructor & Destructor Documentation

template<typename Sample , typename LeftRight >
template<typename Args >
boost::accumulators::impl::peaks_over_threshold_impl< Sample, LeftRight >::peaks_over_threshold_impl ( Args const &  args)
inline

Member Function Documentation

detail::void_ boost::accumulators::accumulator_base::add_ref ( dont_care  )
inlineinherited
detail::void_ boost::accumulators::accumulator_base::drop ( dont_care  )
inlineinherited
detail::void_ boost::accumulators::accumulator_base::on_drop ( dont_care  )
inlineinherited
detail::void_ boost::accumulators::accumulator_base::operator() ( dont_care  )
inlineinherited
template<typename Sample , typename LeftRight >
template<typename Args >
void boost::accumulators::impl::peaks_over_threshold_impl< Sample, LeftRight >::operator() ( Args const &  args)
inline

References boost::program_options::value().

template<typename Sample , typename LeftRight >
template<typename Args >
result_type boost::accumulators::impl::peaks_over_threshold_impl< Sample, LeftRight >::result ( Args const &  args) const
inline

References count, boost::fusion::make_tuple(), pow(), and boost::program_options::value().

The documentation for this struct was generated from the following file: