Iterative calculation of the rolling variance. More...
#include <rolling_variance.hpp>
Public Types | |
| typedef numeric::functional::fdiv < Sample, std::size_t > ::result_type | result_type |
| typedef mpl::false_ | is_droppable |
Public Member Functions | |
| template<typename Args > | |
| immediate_rolling_variance_impl (Args const &args) | |
| template<typename Args > | |
| void | operator() (Args const &args) |
| template<typename Args > | |
| result_type | result (Args const &args) const |
| detail::void_ | operator() (dont_care) |
| detail::void_ | add_ref (dont_care) |
| detail::void_ | drop (dont_care) |
| detail::void_ | on_drop (dont_care) |
Iterative calculation of the rolling variance.
Iterative calculation of sample variance 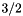 is done as follows, see also http://en.wikipedia.org/wiki/Algorithms_for_calculating_variance. For a rolling window of size
is done as follows, see also http://en.wikipedia.org/wiki/Algorithms_for_calculating_variance. For a rolling window of size 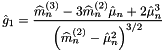 , for the first
, for the first  samples, the variance is computed according to the formula
samples, the variance is computed according to the formula
![\[ \sigma_n^2 = \frac{1}{n-1} \sum_{i = 1}^n (x_i - \mu_n)^2 = \frac{1}{n-1}M_{2,n}, \]](form_58.png)
where the sum of squares  can be recursively computed as:
can be recursively computed as:
![\[ M_{2,n} = \sum_{i = 1}^n (x_i - \mu_n)^2 = M_{2,n-1} + (x_n - \mu_n)(x_n - \mu_{n-1}), \]](form_60.png)
and the estimate of the sample mean as:
![\[ \mu_n = \frac{1}{n} \sum_{i = 1}^n x_i = \mu_{n-1} + \frac{1}{n}(x_n - \mu_{n-1}). \]](form_61.png)
For further samples, when the rolling window is fully filled with data, one has to take into account that the oldest sample  is dropped from the window. The sample variance over the window now becomes:
is dropped from the window. The sample variance over the window now becomes:
![\[ \sigma_n^2 = \frac{1}{N-1} \sum_{i = n-N+1}^n (x_i - \mu_n)^2 = \frac{1}{n-1}M_{2,n}, \]](form_63.png)
where the sum of squares  now equals:
now equals:
![\[ M_{2,n} = \sum_{i = n-N+1}^n (x_i - \mu_n)^2 = M_{2,n-1} + (x_n - \mu_n)(x_n - \mu_{n-1}) - (x_{n-N} - \mu_n)(x_{n-N} - \mu_{n-1}), \]](form_64.png)
and the estimated mean is:
![\[ \mu_n = \frac{1}{N} \sum_{i = n-N+1}^n x_i = \mu_{n-1} + \frac{1}{n}(x_n - x_{n-N}). \]](form_65.png)
Note that the sample variance is not defined for 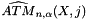 .
.
|
inherited |
| typedef numeric::functional::fdiv<Sample, std::size_t>::result_type boost::accumulators::impl::immediate_rolling_variance_impl< Sample >::result_type |
|
inline |
|
inlineinherited |
|
inlineinherited |
|
inlineinherited |
|
inlineinherited |
|
inline |
|
inline |
References boost::accumulators::extract::rolling_count.