Interface and implementation of BLAS level 3 This includes functions which perform matrix-matrix operations.
More...
|
| template<class M1 , class T , class M2 , class M3 > |
| M1 & | tmm (M1 &m1, const T &t, const M2 &m2, const M3 &m3) |
| | triangular matrix multiplication 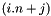 where where 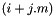 and and 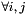 are triangular More... are triangular More...
|
| |
| template<class M1 , class T , class M2 , class C > |
| M1 & | tsm (M1 &m1, const T &t, const M2 &m2, C) |
| | triangular solve 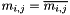 in place, in place, 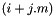 is a triangular matrix More... is a triangular matrix More...
|
| |
| template<class M1 , class T1 , class T2 , class M2 , class M3 > |
| M1 & | gmm (M1 &m1, const T1 &t1, const T2 &t2, const M2 &m2, const M3 &m3) |
| | general matrix multiplication 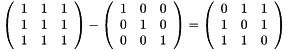 More... More...
|
| |
| template<class M1 , class T1 , class T2 , class M2 > |
| M1 & | srk (M1 &m1, const T1 &t1, const T2 &t2, const M2 &m2) |
| | symmetric rank k update: 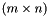 More... More...
|
| |
| template<class M1 , class T1 , class T2 , class M2 > |
| M1 & | hrk (M1 &m1, const T1 &t1, const T2 &t2, const M2 &m2) |
| | hermitian rank k update: 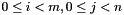 More... More...
|
| |
| template<class M1 , class T1 , class T2 , class M2 , class M3 > |
| M1 & | sr2k (M1 &m1, const T1 &t1, const T2 &t2, const M2 &m2, const M3 &m3) |
| | generalized symmetric rank k update: 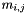 More... More...
|
| |
| template<class M1 , class T1 , class T2 , class M2 , class M3 > |
| M1 & | hr2k (M1 &m1, const T1 &t1, const T2 &t2, const M2 &m2, const M3 &m3) |
| | generalized hermitian rank k update: * 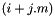 More... More...
|
| |
Interface and implementation of BLAS level 3 This includes functions which perform matrix-matrix operations.
More information about BLAS can be found at http://en.wikipedia.org/wiki/BLAS
template<class M1 , class T1 , class T2 , class M2 , class M3 >
| M1& boost::numeric::ublas::blas_3::gmm |
( |
M1 & |
m1, |
|
|
const T1 & |
t1, |
|
|
const T2 & |
t2, |
|
|
const M2 & |
m2, |
|
|
const M3 & |
m3 |
|
) |
| |
general matrix multiplication 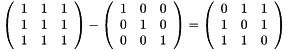
- Parameters
-
| m1 | first matrix |
| t1 | first scalar |
| t2 | second scalar |
| m2 | second matrix |
| m3 | third matrix |
- Returns
- the matrix
m1
- Template Parameters
-
| M1 | type of the first matrix (not needed by default) |
| T1 | type of the first scalar (not needed by default) |
| T2 | type of the second scalar (not needed by default) |
| M2 | type of the second matrix (not needed by default) |
| M3 | type of the third matrix (not needed by default) |
References boost::numeric::ublas::prod().
template<class M1 , class T1 , class T2 , class M2 , class M3 >
| M1& boost::numeric::ublas::blas_3::hr2k |
( |
M1 & |
m1, |
|
|
const T1 & |
t1, |
|
|
const T2 & |
t2, |
|
|
const M2 & |
m2, |
|
|
const M3 & |
m3 |
|
) |
| |
template<class M1 , class T1 , class T2 , class M2 , class M3 >
| M1& boost::numeric::ublas::blas_3::sr2k |
( |
M1 & |
m1, |
|
|
const T1 & |
t1, |
|
|
const T2 & |
t2, |
|
|
const M2 & |
m2, |
|
|
const M3 & |
m3 |
|
) |
| |
generalized symmetric rank k update: 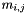
- Parameters
-
| m1 | first matrix |
| t1 | first scalar |
| t2 | second scalar |
| m2 | second matrix |
| m3 | third matrix |
- Returns
- matrix
m1
- Template Parameters
-
| M1 | type of the first matrix (not needed by default) |
| T1 | type of the first scalar (not needed by default) |
| T2 | type of the second scalar (not needed by default) |
| M2 | type of the second matrix (not needed by default) |
| M3 | type of the third matrix (not needed by default) |
- Todo:
- use opb_prod()
References boost::numeric::ublas::prod(), and boost::numeric::ublas::trans().
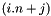 where
where 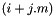 and
and 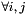 are triangular More...
are triangular More...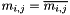 in place,
in place, 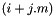 is a triangular matrix More...
is a triangular matrix More...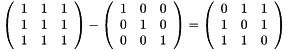 More...
More...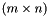 More...
More...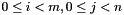 More...
More...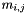 More...
More...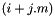 More...
More...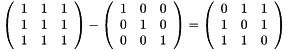
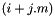
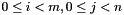
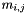
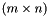
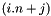 where
where 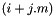 and
and 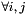 are triangular
are triangular 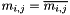 in place,
in place, 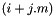 is a triangular matrix
is a triangular matrix 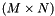 matrix
matrix