Interface and implementation of BLAS level 2 This includes functions which perform matrix-vector operations. More...
Functions | |
| template<class V , class M > | |
| V & | tmv (V &v, const M &m) |
multiply vector v with triangular matrix m More... | |
| template<class V , class M , class C > | |
| V & | tsv (V &v, const M &m, C) |
solve 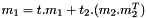 in place, where in place, where m is a triangular matrix More... | |
| template<class V1 , class T1 , class T2 , class M , class V2 > | |
| V1 & | gmv (V1 &v1, const T1 &t1, const T2 &t2, const M &m, const V2 &v2) |
compute 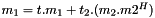 , a general matrix-vector product More... , a general matrix-vector product More... | |
| template<class M , class T , class V1 , class V2 > | |
| M & | gr (M &m, const T &t, const V1 &v1, const V2 &v2) |
Rank 1 update: 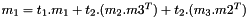 . More... . More... | |
| template<class M , class T , class V > | |
| M & | sr (M &m, const T &t, const V &v) |
symmetric rank 1 update: 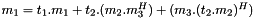 More... More... | |
| template<class M , class T , class V > | |
| M & | hr (M &m, const T &t, const V &v) |
hermitian rank 1 update: 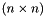 More... More... | |
| template<class M , class T , class V1 , class V2 > | |
| M & | sr2 (M &m, const T &t, const V1 &v1, const V2 &v2) |
symmetric rank 2 update: 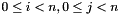 More... More... | |
| template<class M , class T , class V1 , class V2 > | |
| M & | hr2 (M &m, const T &t, const V1 &v1, const V2 &v2) |
hermitian rank 2 update: 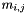 More... More... | |
Interface and implementation of BLAS level 2 This includes functions which perform matrix-vector operations.
More information about BLAS can be found at http://en.wikipedia.org/wiki/BLAS
| V1& boost::numeric::ublas::blas_2::gmv | ( | V1 & | v1, |
| const T1 & | t1, | ||
| const T2 & | t2, | ||
| const M & | m, | ||
| const V2 & | v2 | ||
| ) |
compute 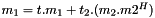 , a general matrix-vector product
, a general matrix-vector product
| v1 | a vector |
| t1 | a scalar |
| t2 | another scalar |
| m | a matrix |
| v2 | another vector |
v1 with the result from the above operation| V1 | type of first vector (not needed by default) |
| T1 | type of first scalar (not needed by default) |
| T2 | type of second scalar (not needed by default) |
| M | type of matrix (not needed by default) |
| V2 | type of second vector (not needed by default) |
References boost::numeric::ublas::prod().
| M& boost::numeric::ublas::blas_2::gr | ( | M & | m, |
| const T & | t, | ||
| const V1 & | v1, | ||
| const V2 & | v2 | ||
| ) |
Rank 1 update: 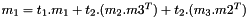 .
.
| m | a matrix |
| t | a scalar |
| v1 | a vector |
| v2 | another vector |
| M | type of matrix (not needed by default) |
| T | type of scalar (not needed by default) |
| V1 | type of first vector (not needed by default) |
| V2type | of second vector (not needed by default) |
References boost::numeric::ublas::outer_prod().
Referenced by boost::graph::distributed::fleischer_hendrickson_pinar_strong_components_impl(), boost::math::octonion< T >::operator*=(), and boost::math::octonion< T >::operator/=().
| M& boost::numeric::ublas::blas_2::hr | ( | M & | m, |
| const T & | t, | ||
| const V & | v | ||
| ) |
hermitian rank 1 update: 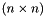
| m | a matrix |
| t | a scalar |
| v | a vector |
| M | type of matrix (not needed by default) |
| T | type of scalar (not needed by default) |
| V | type of vector (not needed by default) |
References boost::numeric::ublas::conj(), and boost::numeric::ublas::outer_prod().
Referenced by boost::chrono::detail::extract_z(), boost::math::octonion< T >::operator*=(), boost::math::octonion< T >::operator/=(), boost::spirit::intersection< A, B >::parse(), and boost::spirit::difference< A, B >::parse().
| M& boost::numeric::ublas::blas_2::hr2 | ( | M & | m, |
| const T & | t, | ||
| const V1 & | v1, | ||
| const V2 & | v2 | ||
| ) |
hermitian rank 2 update: 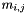
| m | a matrix |
| t | a scalar |
| v1 | a vector |
| v2 | another vector |
| M | type of matrix (not needed by default) |
| T | type of scalar (not needed by default) |
| V1 | type of first vector (not needed by default) |
| V2type | of second vector (not needed by default) |
References boost::numeric::ublas::scalar_traits< T >::conj(), boost::numeric::ublas::conj(), and boost::numeric::ublas::outer_prod().
| M& boost::numeric::ublas::blas_2::sr | ( | M & | m, |
| const T & | t, | ||
| const V & | v | ||
| ) |
symmetric rank 1 update: 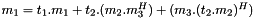
| m | a matrix |
| t | a scalar |
| v | a vector |
| M | type of matrix (not needed by default) |
| T | type of scalar (not needed by default) |
| V | type of vector (not needed by default) |
References boost::numeric::ublas::outer_prod().
| M& boost::numeric::ublas::blas_2::sr2 | ( | M & | m, |
| const T & | t, | ||
| const V1 & | v1, | ||
| const V2 & | v2 | ||
| ) |
symmetric rank 2 update: 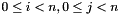
| m | a matrix |
| t | a scalar |
| v1 | a vector |
| v2 | another vector |
| M | type of matrix (not needed by default) |
| T | type of scalar (not needed by default) |
| V1 | type of first vector (not needed by default) |
| V2type | of second vector (not needed by default) |
References boost::numeric::ublas::outer_prod().
| V& boost::numeric::ublas::blas_2::tmv | ( | V & | v, |
| const M & | m | ||
| ) |
multiply vector v with triangular matrix m
| v | a vector |
| m | a triangular matrix |
| V | type of the vector (not needed by default) |
| M | type of the matrix (not needed by default) |
References boost::numeric::ublas::prod().
| V& boost::numeric::ublas::blas_2::tsv | ( | V & | v, |
| const M & | m, | ||
| C | |||
| ) |
solve 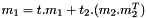 in place, where
in place, where m is a triangular matrix
| v | a vector |
| m | a matrix |
| C | (this parameter is not needed) |
| V | type of the vector (not needed by default) |
| M | type of the matrix (not needed by default) |
| C | n/a |
References boost::numeric::ublas::solve().